The development of an enterprise is always associated with economic risks, implying either failure to receive the expected benefits or the financial crisis of the company with the threat of closure. For this reason, before any expansion, it is necessary to conduct analytical work aimed at the mathematical calculation of profitability, justification, and profitability of such actions (Cleaves et al., 2013).
This work is characterized by a case study in which the head of the company plans to make two large purchases in the next five years – a warehouse and a molding machine for the production of vinyl enclosures. Both purchases are expensive, so the head of the company makes decisions about annuity rent and depreciation fund. For the purchase of warehouse space, the insurance company proposes considering two promising options: an annuity and an annuity due. At the same time, the molding machine has a service life after which it fails – to save on the purchase in three years, it is proposed to use the depreciation fund, which provides benefits up to 12% per annum. This essay aims to make a mathematical calculation of the described cases and to find out which option would be more advantageous for the entrepreneur.
Buying Warehouse Space
Before proceeding with mathematical calculations, it should be recalled that annuity is a term widely used in recent decades in the field of credit. In general terms, an annuity is understood to be a payment scheme according to which it is made at the same rate according to a specific payment schedule. In particular, payments are made on an ongoing basis at equal intervals, such as every month, quarter, six months, or year. In simple words, an annuity can be represented as a flow of equivalent payments at equal time intervals. An annuity payment consists of two payments: a percentage for the use of goods and a balance for the debt (Cleaves et al., 2013).
According to Surbhi (2016), the difference between an ordinary annuity and an annuity due lies in the mechanics of payments. While ordinary annuity implies payment at the end of the billing period, in an annuity due, the payment is made at the beginning. This may seem insignificant, but the financial difference between such technologies is enormous.
The number of accounting periods required for the annuity must be clarified before making the calculations. It is five years, but the payment is made every quarter. In that case, the number of periods will be equal to:
![]()
At the same time, the annual interest rate is 8%, which means that the amount rises long according to the formula every quarter:
![]()
Bearing in mind that an equivalent payment of $2,500.00 is made every quarter, a formula for a regular annuity is drawn up (Table 1). As can be seen from the given data, the total payment in five years will make $60,743.42. A similar calculation is necessary for the second type of payment when payment is made at the beginning of the accounting period (Table 2). Table 2 shows that the total amount of payments will be $61,958.29. It is not difficult to determine that the second variant is more advantageous under the same credit conditions, because it assumes an increase in the total cost by $1,214.87 while retaining the terms. Moreover, interest under chosen annuity needs to be calculated – for this case, it is an annuity due of $61,958.29:
![]()
![]()
Table 1: Schedule of annuity payments at repayment of debts at the end of the quarter
Table 2: Schedule of annuity payments at repayment of debts at the beginning of the quarter
Buying a Molding Machine
The prospects for future credit obligations burden the enterprise’s economic sector, so depreciation funds are used to mitigate this. In general, it should be understood that such funds are cash accumulated from depreciation charges of property, plant, and equipment designed to restore worn-out assets and acquire new ones. It is essential to recognize that the depreciation fund is created to accumulate, at the expense of accrued depreciation, cash assets whose primary purpose is to replace, modernize and repair obsolete, worn-out or decommissioned fixed assets.
This also applies to molding devices used to produce vinyl fences. It is known that in three years, the entrepreneur will have to pay $45,000.00. It is typical for this company that the depreciation fund is formed twice a year and earns a 12% annual rate. Accordingly, the interest rate for one period can be calculated by the formula:
![]()
According to the “Sinking fund formula” (n.d.), the periodic contribution to the depreciation fund is calculated as follows:
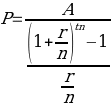
where A is the amount to be repaid in the future, r is the annual interest rate, n is the number of periods per year and t is the number of years.
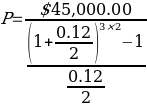
![]()
Finally, the calculation on the interest which is earned on the sinking fund is made according to the formula:
![]()
![]()
![]()
![]()
As can be seen from the calculations, the interest in the Sinking Fund is almost half as much as the annuity payment. In other words, shorter terms with higher payments guarantee that quarterly payments will be smaller, so the load on companies will be lower (Murphy, 2019). Based on the data, it is not difficult to conclude that the molding machine needs to be replaced in the first place, and the remaining cash may go into backup storage to expand the storage network in the future. Moreover, if companies now concentrate on expanding their warehouses, in three years, there may be a collapse caused by the downtime of the storage facilities due to the failure of the molding machine.
References
Cleaves, C., Hobbs, M., & Noble, J. (2013). Business math brief: Pearson new international edition. Pearson Higher Ed.
Murphy, Chris B. (2019). Sinking fund. Investopedia. Web.
Sinking fund formula. (n.d.). EDUCBA. Web.
Surbhi, S. (2016). Difference between ordinary annuity and annuity due. Key Difference. Web.
