Introduction
Weather derivatives are the financial instruments used by either individuals or organizations as a partial strategy to risk management aimed at reducing the risk or risks associated with unpredictable adverse weather conditions. The cardinal difference between weather derivatives and the other derivatives is that the aspect in question bears no direct value to the weather derivative used. Farmers may find the use of derivatives useful in shielding them against harsh weather and possibly act on time before their crops are destroyed by weather extremes. Sporting companies may also find weather derivatives useful while carrying out their activities like the sale of tickets which may be affected by harsh weather. On a day when they predict that the weather will be harsh, they refrain from selling the tickets waiting for a weather-friendly day to make the sales. This will ensure that they make more sales than they would have made if they did not rely on the weather observations made by researchers like this one.
Slowly the weather derivatives gained popularity and started trading more freely in the United States, Europe, Japan and Canada. In most cases, weather derivatives are priced using analysis of some historical output of a given weather index. Statistical techniques are therefore used in evaluating the methods to be used in the analysis of a given data which is to be priced. Weather derivatives are mainly used in controlling and analyzing risks that naturally give rise to weather. Most businesses are dependent on weather outcomes and therefore benefit immensely from weather derivatives. The most affected of these are the energy-producing and consuming companies, supermarket chains and both agricultural and industrial companies. The supermarket chains decide on what to stock in their shops by sometimes observing the weather patterns. If the weather is dry they stock goods that go with such a service. Likewise when the weather is wet and humid, the supermarkets stock those goods that are mostly required during the wet weather. Examples of goods that are sold during wet weather include raincoats and gumboots just to mention a few.
Objectives
This research aims to observe both major objectives and minor objectives after their successful completion are mentioned below.
Main Objectives
The main objective of this study is to explore the methods that can be used to analyze data from varying weather conditions. These include temperatures, rainfall and humidity among others. However, particular attention is given to temperatures and the study is directed to advanced analysis of the same. The scope of the data in question though is limited to Kansas, a city in Missouri State in the United States. The successful completion of this research should lead to a conclusive end on search for a better way to analyze the weather conditions of a given place and use it to make wise decisions regarding the future behavior of elements of weather.
Minor Objectives
Among other objectives that this research is intended to achieve is establishing the relationship between two or more variables that compare weather components affecting a given geographical region. Each of these weather elements can be studied separately to come up with a conclusive idea of how the weather of a given place can be predicted to avoid a given adverse phenomenon. The phenomenon may influence the outcome of a given event that is weather dependent like a sporting event whose sale of tickets depends on the weather of the day when the game is being played.
Another objective of this study is to ensure that the research done by this work will help improve the data bank of the information available so far in the archive on similar works done in the past on weather derivatives.
The research will also aid in demystifying the fact that weather is a naturally occurring event and that man can actually do very little to avert the effects of adverse weather happening in the future. It should be noted that old school thought has always been that since supernatural forces are the ones responsible for the varied weather conditions, we may not do much to prepare ourselves for the future effects of weather elements. The adage thought will be no longer valid after the reality unfolds following successful completion of this study.
The study upon successful completion will demystify the old belief that weather patterns that weather conditions are a result of supernatural powers and human beings have little or no control over the same. Inasmuch as most of the conditions are supernaturally controlled and human beings human are only recipients of the weather conditions, a proper analysis of the weather aspects recorded in the past could lead to a better understanding of the weather.
Literature Review
The research on weather and its effects has been widely done in the past by different researchers. Much of what has been done in the past about weather has been properly documented. This paper has not been done with an intention of nullifying what has already been done in the past but intends to add to what has already been done. This will eventually bridge the knowledge gap that may have been left out by researches done in the past. Much of what has been done in the past involves studying the aspects of weather and their possible effects on human life.
Since time immemorial, the weather has been studied with an intention of getting a better understanding of how the weather will behave in future. This would aid a lot in ensuring the proper planning of activities. Agricultural activities have specifically been dependent on the behavior of weather since time immemorial. Activities like planting, weeding and harvesting require proper analysis of the weather to avoid spoiling of harvest.
This paper intends to bring in the mathematical aspect added onto the geographical aspect intending to combine these two to come up with a better understanding of how weather elements can be predicted.
These predictions when done with precision may be of great help to many organizations whose activities are pegged on weather outcomes.
Valuation of Weather Derivatives
Weather derivative valuation involves borrowing information from both meteorology and finances and combining this skillfully with mathematical concepts and to be more specific statistics. It is therefore important for an individual carrying out the valuation to have some good knowledge of statistical analysis skills. It is worth noting that there is no one existing perfect statistical approach to valuation. Several writers though have tried to come up with variety of ways to approach valuation in the best manner possible.
A proper valuation of weather derivatives needs to take place before deciding conclusively to settle on it. It is worth noting that one particular weather derivative may not exactly be replaced by another one that does not match its cost-efficiency. In a way, valuation of weather derivatives compares in several ways to insurance policy pricing methods. It is therefore fundamental to base valuation on sources of data that are reliable so as to come up with indexes that are accurate.
One of the methods of pricing weather derivatives is by use of historical data and then highlighting any challenges that may have come up in the process. The most common of all the derivative methods is the heating degree day (HDD) or the cooling degree day (CDD) category.
The daily cumulative increments are more or less the same as the daily HDD normally defined by:
- HDD i=max (18-Xi, 0),
In that case, Xi is given by the daily average temperatures of the day i recorded during the winter period and generally Xi ≤ 18
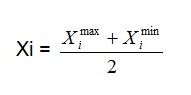
gives the average temperatures recorded on a particular day I and is given in degrees Celsius, with X maxi and X mini given by the maximum and the minimum temperatures measured on a particular day denoted by i.
And therefore HDD i = 18- Xi
It is worth noting therefore that these increments normally show a long-term cycle or trend which is an exact opposite though equal to the average temperatures.
The Cooling Degree Days (CDD) recorded on a day i will be defined by:
- CDD i =max (Xi-18, 0)
At the same time if we suppose that we have a contract period of 0≤t≤T recorded on a number of N days. Then the cumulative number of CDD and HDD for the period given by HN= ![]() and CN=
and CN=![]() respectively.
respectively.
Denoting the strike level using a constant K and the assigning the monetary value paid per degree Celsius a tick, the payoff for an uncapped HDD put as an option as,
- P call =max (HN-K, 0) tick or
- P put =max (K-HN, 0) tick respectively,
Similarly for each uncapped CDD call or put option.
In this method, the researcher has to consider the cumulative heating degree day recorded within the last couple of years. This will become useful in coming up with the hypothesis for the high degree day data he wants to work on as at that moment. The hypothesis once formulated is tested by performing a square test at a given level aimed at obtaining a given percentage level. The results of the percentage should be consistent with the pattern of distribution of the data which in most cases is a normal distribution. At this juncture, both the mean and the standard deviation of the distribution of the cumulative heat degree day are calculated.
The mean is usually abbreviated as (m) while the standard deviation is abbreviated by (s) for easier use in computations which are to come later in the workings. The mean gives the average of the data that is available for computation and for the analysis to be successful finding the mean becomes a very useful exercise. There are several methods that can be used to test the hypothesis for the best fit in the distribution.
The main method used in such a case is by performing the Jarque-Bera test which in most cases works hand in hand with Matlab software to bring out the desired results for the distribution data being used. The results of the tests help in coming up with the desired hypothesis for the distribution and should be in most cases consistent with a normal distribution (Huber, 1981). This will make the approximations and estimations of the daily temperatures to be consistent with a normal distribution once the hypothesis is assumed to be true.
Before using the hypothesis in valuation of the contract in question, it is necessary to identify both the mean and the standard deviation of the daily average increases of the recorded temperatures.
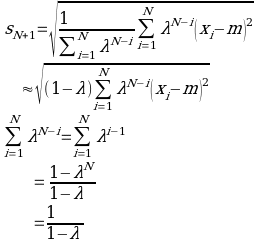
In the above equation, xi=1, 2, 3, 4………….. N and m is the arithmetic mean mainly based on twenty years of historical data. The temperature increment per day is given by i. m is the arithmetic mean of the temperature values
At the same time the mean can be calculated using the following formula. This pays particular attention to the mean of the (N+1) position of the daily increment which is given by:
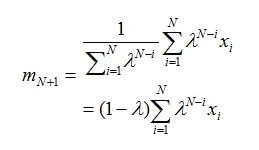
In the formulae above the decay factor is taken as λ and in this case it is equal to 0.78 and this shows a typical decay factor for prices of commodities in the energy sector. The prices are taken to range from 0.7≤λ≤0.9.
When carrying out analysis for temperatures recorded over a long period of time, like thirty days, the mean and the standard deviation of the overall period are calculated. In order to successfully do this, the mean and the standard deviations of the increments for each day are calculated using a thirty-day rolling average. This is successfully done by giving the older temperature rises a lesser weight than the weight that is more recent. In most cases this is referred to as exponentially weighted moving average.
Challenges associated with historical temperature data
There are a number of problems though are associated with the analysis of historical temperatures recorded after a given period of time. One of such problems is that the data may not be complete as some bits of information may have been either lost in the process of retrieving or may have been omitted in totality (Neftci, 2000). It is therefore important to put into consideration that such historical data cannot be flawless.
The other problem is that during a leap year, there is an additional day in the contract year. This calls for additional adjustments to be effected so that the data becomes palatable. In some other cases the weather station may have been moved from the original location to another one that may be having differing weather conditions and this may affect the validity of our data.
The contracts
Most weather derivatives are structured as swaps, call or put and futures and are based on different weather indices. The most commonly used indices are the cooling and heating degree days, rain and in some cases snowfall (Neftci, 2000). Temperature of a given weather station is normally denoted by T![]() which denotes maximum temperatures and T
which denotes maximum temperatures and T![]() which denotes minimum temperatures of a particular day i and is given in degrees Celsius.
which denotes minimum temperatures of a particular day i and is given in degrees Celsius.
The origin of the names heating and cooling degree days is from the United States energy sector. Most of the temperature-based derivatives of weather are based on the actual accumulation of HDD s or CDD s during a particular period which is usually one month or a winter period (Coles, 2001). The HDD season normally runs from November to March whole the CDD period runs from May to September. The period between April and October is normally regarded as the shoulder months of the year.
Another major challenge posed by using historical data is that it is not clear how many years ought to be considered adequate for use in data collected for a given analysis. In some cases, ten years are used while in other cases the period stretches up to about fifty years. This creates an element of controversy in terms of the appropriate time to be considered in a given case of data analysis (Nelken, 2000). Due to the recent effects of global warming, some parts may experience higher temperatures than others and this may affect the behavior of the data to be analyzed. This problem can however be solved by reasonably shifting the data linearly while at the same time ensuring that it does not lose a lot of meaning and value.
There are some adjustments that ought to be carried out before the data is considered fit for use in our analysis. At the back of the mind though, the researcher should remember that the linear shift of data is subjective and therefore need to be used cautiously. This is more so because a linear shift of data leads to a lot of inaccuracies in the data being analyzed.
The other problem occurs when there are extremes of weather patterns like El Nino and La Nina as they may cause variations in the temperatures recorded under normal circumstances. Although these extremes do not occur in all parts of the world, their effect is eventually felt in a majority of the parts of the world.
The table below shows average monthly temperatures recorded for one year in Kansas City, Missouri and other weather indicators like precipitation and snowfall (World temperature records 2003).
Simulation
According to the table above, one can conclude that the lower the average wind speed, the higher the possibility of having a sunny month. The correlation between cloudy months and the average relative humidity is also very high. When the cloud cover increases, the average relative humidity also increases and when cloud cover decreases, the average relative humidity also decreases at the same rate.
Conclusion
In conclusion, the observation that can be made from this study is that weather derivatives are not only necessary in helping forecast temperatures but also other weather conditions as well. This information can be very helpful to those people who carry out activities and businesses that are weather-dependent. The data gathered in this study applies only to the case of Kansas City of Missouri State in the United States of America.
References
Coles, S. (2001). An Introduction to Statistical Modeling of Extreme Values, New York: Springer Verlag
Huber, P.J. (1981). Robust Statistics, New York: John Wiley & Sons
Neftci, S.N. (2000).An introduction to the Mathematics of Financial Derivatives. Academic Press.
Nelken, I. (2000).Weather Derivatives- Pricing and Hedging.Super Computer Consulting, Inc. Web.
